Bei einer Kurvendiskussion wird eine Funktion auf ihre geometrischen Eigenschaften untersucht. Zu diesen zählen charakteristische Punkte des Funktionsgraphen, wie Nullstellen, Hoch- und Tiefpunkte, Wende- und Sattelstellen, Polstellen usw. Gleichzeitig werden charakteristische Eigenschaften de Graphen, wie Symmetrie- und Krümmungsverhalten, sowie das Verhalten im Unendlichen untersucht. Anhand all dieser Punkte und Eigenschaften ist es letztendlich auch möglich, eine Skizze des Funktionsgraphen anzufertigen, welche die markanten Punkte der Funktion und den Verlauf zwischen den Punkten abbildet.
In den vergangenen Artikeln wurden bereits wichtige Elemente einer Kurvendiskussion erläutert, so z.B. die Differenzierbarkeit und Stetigkeit von Funktionen, sowie wichtigen Funktionsuntersuchungen. Das Handwerkzeug einer jeden Kurvendiskussion ist die Ableitung von Funktionen. Es ist daher wichtig, die Ableitungsregeln zu beherrschen (oder zumindest zu wissen, wo sie stehen ;)) und diese zur Klausurvorbereitung idealerweise auswendig zu lernen und anhand von Ableitungsbeispielen zu üben.
In diesem fünften und letzten Teil der Artikelreihe „Differentialrechnung in 5 Schritten“ soll eine vollständige Kurvendiskussion anhand eines Beispiels durchgeführt werden.
Systematische Kurvendiskussion
Bei einer systematischen Kurvendiskussion rechnet man nicht einfach irgendwo drauf los, sondern geht – wie der Name es bereits verrät – nach System vor. „System“ bedeutet in dem Fall, dass eine schrittweise Untersuchung der Funktion stattfindet. In der Regel werden im Rahmen einer Kurvendiskussion folgende 11 Punkte untersucht:
- Festlegung des Definitionsbereichs
- Festlegung des Stetigkeits- und Differenzierbarkeitsbereiches
- Bestimmung der ersten drei Ableitungen
- Untersuchung der Funktion an den Rändern des Definitionsbereichs. Dazu gehören die äußeren Ränder (Asymptoten), sowie mögliche Definitionslücken (Polstellen).
- Bestimmung der Nullstellen
- Bestimmung der Extremstellen und der dazugehörigen Extrema
- Bestimmung der Wendestellen und der dazugehörigen Wendepunkte
- Untersuchung des Monotonieverhaltens
- Untersuchung des Krümmungsverhaltens
- Berechnung spezieller Funktionswerte
- Zeichnung des Funktionsgraphen
Das ist die mathematische Funktionsweise einer Kurvendiskussion, welche im folgenden an einem Beispiel Schritt für Schritt durchgeführt werden soll.
Beispiel: f(x) = 5x³ – 2x² + 4x – 7
1. Festlegung des Definitionsbereichs
Bei unserem Beispiel handelt es sich um eine ganzrationale Funktion dritten Grades. Bei der Festlegung des Definitionsbereichs gilt es jetzt zu prüfen, ob die Funktion überall definiert ist oder ob es an irgendeiner Stelle Ausnahmen gibt.
Eine ganzrationale Funktion, wie in unserem Beispiel ist auf der Menge der Reellen Zahlen IR definiert. Egal, welche reelle Zahl man für x einsetzt, es existiert ein y-Wert.
Man schreibt für den Definitionsbereich dann: ID = IR.
Anders verhält es sich bei gebrochen rationalen Funktionen. Sollten Polstellen vorhanden sein, ist die Funktion auf der Menge der Reellen Zahlen definiert, mit Ausnahme der Polstellen: ID = IR\{„Pole“}. Neben diesem Fall gibt es auch noch weitere Ursachen für eingeschränkte Definitionsbereiche und Definitionslücken, wie ungerade Wurzeln für negative Zahlen, Logarithmusfunktionen für negative Zahlen oder Teilen durch Null. Diese treffen auf unser Beispiel jedoch nicht zu.
2. Festlegung des Stetigkeits- und Differenzierbarkeitsbereiches
Differenzierbar bedeutet, dass eine Funktion an einer bestimmten Stelle ableitbar ist. Formal sagt man, dass der Grenzwert des Differenzenquotienten existieren muss:
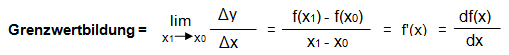
Ist eine Funktion differenzierbar, so ist sie auch stetig. Die Stetigkeit muss man sich bildlich so vorstellen, dass der Funktionsgraph durchgehend gezeichnet werden kann, ohne den Stift abzusetzen. Ist eine Funktion an einem bestimmten Punkt nicht stetig, z.B. weil dort eine Lücke ist, so ist sie dort auch nicht differenzierbar.
Um an einer Stelle differenzierbar zu sein MUSS die Funktion dort also stetig sein. Allerdings gilt das nicht zwingend für den umgekehrten Fall. Ist eine Funktion stetig, KANN sie, muss aber nicht zwingend auch differenzierbar sein.
Wenn wir uns die Funktion f(x) = 5x³ – 2x² + 4x – 7 anschauen, gilt es jetzt zu überlegen, ob es Bereiche gibt, an denen die Funktion nicht ableitbar ist. Dies ist nicht der Fall.
Zur Differenzierbarkeit kann man sich diese beiden Sätze merken:
– Jedes Polynom ist differenzierbar über ganz IR.
– Jede gebrochen rationale Funktion ist differenzierbar über ihrem Definitionsbereich.
3. Bestimmung der ersten drei Ableitungen
Die ersten drei Ableitungen der Funktion sind wichtig, da sie Aufschluss über markante Punkte und Eigenschaften der Funktion geben, die in den kommenden Punkten behandelt werden.
Die ersten drei Ableitungen der Funktion f(x) = 5x³ – 2x² + 4x – 7 lauten:
f'(x) = 15x² – 4x + 4
f“(x) = 30x – 4
f“'(x) = 30
4. Untersuchung der Funktion an den Rändern des Definitionsbereichs
Bei der Untersuchung einer Funktion an den Rändern des Definitionsbereichs untersucht man die Funktion an den äußeren Ränder (d.h. Asymptoten), sowie an den eventuell gefundenen Polstellen.
Wie unter Punkt 1 bereits festgestellt, hat die Funktion f(x) = 5x³ – 2x² + 4x – 7 keine Pole, und auch keine Asymptoten, da sie auf der Menge der Reellen Zahlen definiert ist. Die Ränder des Definitionsbereichs sind in unserem Fall ±∞.
Man setzt für x also eine möglichst hohe und eine möglichst niedrigere Zahl ein und schaut, ob die Funktion gegen +∞ oder -∞ strebt:
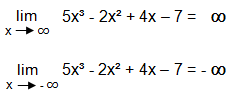
Strebt x gegen +∞, so strebt auch der Grenzwert der Funktion f(x) gegen +∞. Strebt x gegen -∞, so strebt auch der Funktionswert gegen -∞.
5. Bestimmung der Nullstellen
Für welche x-Werte wird f(x) gleich Null? Diese Frage lässt – je nach Funktionstyp – mal leichter, mal schwerer beantworten. Bei Funktionen zweiten Grades lassen sich die Nullstellen direkt mit der p-q-Formel oder durch Umwandlung der Funktion in die Form f(x) = (x+a)(x+b) ermitteln.
Bei Funktionen dritten (oder höheren) Grades, wie wir sie in unserem Beispiel vorfinden ist es schon etwas schwieriger, die Nullstellen herauszufinden. Da die Anzahl der Nullstellen aber immer dem höchsten Grad der Funktion entspricht (hier x³), haben wir es in unserem Fall mit drei Nullstellen zu tun.
Zunächst versucht man, sich der ersten Nullstelle durch Probieren zu nähern. Man nennt das Verfahren daher auch Näherungsverfahren. Hierfür setzt man beliebige x-Werte in die Funktion f(x) = 5x³ – 2x² + 4x – 7 ein und ermittelt die entsprechenden y-Werte. Setzen wir in unserem Funktion z.B. die x1 = 2 und x2= -2 ein. Wir erhalten y1= 33 und y2= -63. Da die Funktionswerte vom positiven in den negativen Bereich wechseln, muss dazwischen eine Nullstelle liegen. (Voraussetzung ist natürlich, dass die Funktion zwischen -2 < x < 2 auch definiert ist.) Als nächsten Schritt können wir den Bereich verkleinern und x3 = 1 und x4= -1 in die Funktion einsetzen.
Wir setzen zunächst x3 = 1 in die Funktion ein und stellen fest:
f(1) = 5(1)³ – 2(1)² + 4(1) – 7
f(1) = 5 – 2 + 4 – 7
f(1) = 0
Bei x=1 wird die Funktion Null, wir haben die erste Nullstelle also gefunden. Oft kann es etwas länger dauern, bis man eine Nullstelle gefunden hat, man sollte den Bereich der x-Werte jedoch nicht zu groß wählen. Wenn eine Funktion keine konstante Zahl, wie hier die 7 enthält, so ist die erste Nullstelle schon mal immer die Null. Dann kann man sich das zeitraubende Suchen direkt sparen.
Hat man die erste Nullstelle gefunden, kann man das Polynom durch Division mit „x-Nullstelle) zerlegen. Man nennt diese Rechenoperation auch Polynomdivision. Ziel der Polynomdivision ist es, aus unserer Funktion dritten Grades eine Funktion zweiten Grades zu machen und die anderen beiden Nullstellen anschließend mit der p-q-Formel auszurechnen.
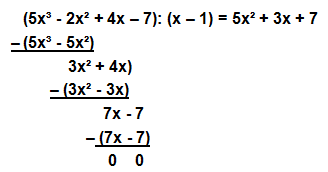
Zunächst teilen wir 5x³ durch x und erhalten 5x², den ersten Term der Lösung. Anschließend multiplizieren wir 5x² mit (x-1) und subtrahieren dieses Ergebnis von der Funktion. 5x³ löst sich auf, als Ergebnis erhalten wir 3x². Jetzt beginnen wir wieder von Vorne und teilen 3x² durch x. Das Ergebnis, 3x wird wieder mit (x-1) multipliziert und anschließend abgezogen. So geht man weiter vor, bis die Polynomdivision beendet ist.
Das Ergebnis lässt sich anhand einer Probe schnell überprüfen:
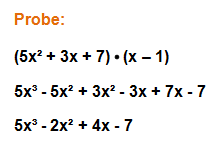
Das Ergebnis ist identisch mit der Originalfunktion, wir haben also richtig gerechnet. Nun können wir mit der quadratischen Funktion die p-q-Formel anwenden und die restlichen beiden Nullstellen berechnen. Hierfür teilen wir die Funktion zunächst durch 5 und bringen sie so in „Normalform“.
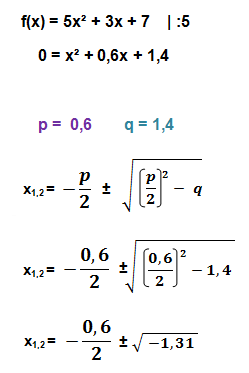
Da in der Wurzel ein negativer Term steht, eine negative Wurzel im Bereich der reellen Zahlen jedoch nicht definiert ist, können wir an dieser Stelle abbrechen. Die Funktion f(x) = 5x³ – 2x² + 4x – 7 hat somit nur eine Nullstelle bei x=1. Würde in der Wurzel eine Null stehen, gäbe es bei der p-q-Formel genau eine Lösung, bzw. dann insgesamt zwei Nullstellen.
6. Bestimmung der Extremstellen und der dazugehörigen Extrema
Ein weiterer wesentlicher Bestandteil der Kurvendiskussion ist die Bestimmung von Extremstellen (Hoch- und Tiefpunkte) und der dazugehörigen Extrema (y-Werte). Hierzu setzt man die erste Ableitung f'(x) gleich Null. Dort, wo die erste Ableitung der Funktion Nullstellen hat, hat die Originalfunktion f(x) Extremstellen. ABER: Es kann auch Stellen geben, an denen die erste Ableitung zwar Null wird, die Originalfunktion aber keine Extremstellen besitzt. Dies ist dann der Fall, wenn auch die zweite Ableitung gleich Null wird. Dann handelt es sich um eine sogenannte „Sattelstelle“.
Ist f'(x) = 0, f“(x) = 0, handelt es sich um eine Sattelstelle.
Ist f'(x) = 0, f“(x) ≠ 0, handelt es sich um eine Extremstelle.
Auch hier können wir die Ergebnisse bequem mit der p-q-Formel ermitteln:
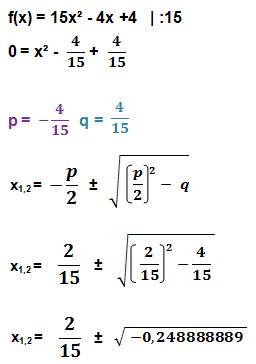
Da in der Wurzel eine negative Zahl steht, hat die erste Ableitung keine Nullstellen und die Funktion 5x³ – 2x² + 4x – 7 somit auch keine Hoch- und Tiefpunkte.
7. Bestimmung der Wendestellen und der dazugehörigen Wendepunkte
An einer Wendestelle wechselt oder „wendet“ eine Funktion ihre Krümmung, z.B. von einer Rechts- zu einer Linkskrümmung. Zur Bestimmung der Wendestellen benötigen wir die zweite und dritte Ableitung.
Eine Wendestelle ist vorhanden, wenn gilt:
f“(x) = 0 (notwendiges Kriterium)
f“'(x) = 0 ^ f“'(x) ≠ 0 (hinreichendes Kriterium)
Hat die zweite Ableitung an einer Stelle x eine Nullstelle und die dritte Ableitung nicht, so haben wir es mit einer Wendestelle zu tun. Überprüfen wir das mal für unser Beispiel. Die zweite Ableitung lautet:
f“(x) = 30x – 4
0 = 30x – 4
-30x = -4
x = 0,1333
Setzen wir das Ergebnis nun in die dritte Ableitung ein:
f“'(0,1333) = 30
Da es sich bei der dritten Ableitung um eine Konstante handelt, die keine Nullstellen hat, befindet sich bei x= 0,1333 eine Wendestelle. Eingesetzt in 5x³ – 2x² + 4x – 7 erhalten wir auch die genauen Koordinaten der Wendestelle bei W=(0,1333 | -6,4903).
8. Untersuchung des Monotonieverhaltens
Bislang haben wir im Rahmen dieser Kurvendiskussion charakteristische Punkte der Funktion betrachtet. In den folgenden beiden Abschnitten beschäftigen wir uns mit dem Verlauf der Funktion zwischen diesen Punkten.
Bei der Untersuchung des Monotonieverhaltens unterscheidet man zwischen steigenden, streng steigenden, fallenden und streng fallenden Funktionen. Um herauszufinden, in welchen Intervallen der Funktionsgraph wie verläuft, nutzt man die erste Ableitung f'(x)= 15x² – 4x + 4.
Es gilt:
f'(x) ≥ 0 = monoton steigend
f'(x) > 0 = streng monoton steigend
f'(x) ≤ 0 = monoton fallend
f'(x) < 0 = streng monoton fallend
Wie geht man nun vor? Zunächst stellt man Intervalle auf. Dabei werden wie vor allem Extremstellen und Sattelstellen als charakteristische Punkte der Funktion berücksichtigt. Denn zwischen Hoch- und Tiefpunkten ist eine Funktion immer streng monoton fallend. Wenn dazwischen ein Sattelpunkt liegt, ist sie nur monoton fallend.
Da unsere Funktion allerdings keine Extremstellen hat, weil die erste Ableitung keine Nullstellen besitzt, ist sie auch an keiner Stelle streng monoton steigend, bzw. fallend. Diese beiden Fälle können wir schon mal ausschließen.
Bleibt nur zu schauen, ob die Funktion monoton steigend oder monoton fallend ist. Setzt man nun verschiedene positive und negative x-Werte in die Ableitungsfunktion ein, so stellt man fest, dass stets gilt: f'(x) > 0. Damit ist unsere Funktion monoton steigend.
Wie unter Punkt 7 bestimmt, besitzt die Funktion f(x) = 5x³ – 2x² + 4x – 7 aber bei x = 0,1333 eine Wendestelle. Dort ändert sie also ihre Krümmung. Dies hat allerdings in unserem Fall keine Auswirkung auf die Monotonie, da die Originalfunktion an der Wendestelle zwar ihre Krümmung, aber nicht ihr Monotonieverhalten ändert.
Die Funktion ist daher für -∞ ≤ x ≤ ∞ monoton steigend.
9.Untersuchung des Krümmungsverhaltens
Bei der Untersuchung des Krümmungsverhaltens geht es darum zu schauen, in welchem Intervall eine Funktion linksgekrümmt (konvex), bzw. rechtsgekrümmt (konkav) ist. Bei einem konvexen Funktionsverlauf (gegen den Uhrzeigersinn) ist die Funktion nach oben geöffnet und dreht sich gegen den Uhrzeigersinn, bei einem konkaven Verlauf (im Uhrzeigersinn) hingegen ist sie nach unten geöffnet, mit Drehung gegen den Uhrzeigersinn. Um das Krümmungsverhalten zu bestimmen, nutzt man die zweite Ableitung f“ (x) = 30x – 4.
Es gilt:
f“(x) > 0 = Linkskrümmung (konvex, nach oben offen)
f“(x) < 0 = Rechtskrümmung (konkav, nach unten offen)
Wie eben erwähnt, wird die zweite Ableitung bei x = 0,1333 gleich Null. Dort haben wir eine Wendestelle. Für alle x < 0,1333 wird f“(x) < 0, für alle x > 0,1333 wird f“(x) > 0. Zusammenfassend kann mal also sagen:
f(x) ist für -∞ ≤ x ≤ 0,1333 konkav, also rechtsgekrümmt.
f(x) ist für 0,1333 ≤ x ≤ +∞ konvex, also linksgekrümmt.
An der Wendestelle x = 0,1333 ist die Funktion gerade und hat keine Krümmung.
10. Berechnung spezieller Funktionswerte
Um den Funktionsgraphen besser zeichnen zu können, empfiehlt es sich, eine Wertetabelle anzulegen und spezielle Funktionswerte zu berechnen (z.B. x=0). Wie viele Werte man berechnet, hängt von der Funktion ab. Bei einfachen Funktionen reichen oft schon etwa 5-7 Werte, bei komplexeren Funktionen sollte es schon das Doppelte sein.
Für unsere Funktion f(x) = 5x³ – 2x² + 4x – 7 reicht eine relativ kleine Wertetabelle aus. Setzt man probeweise einige x-Werte in die Funktion ein, so stellt man fest, dass sie von -3 > x > 3 sehr hohe Funktionswerte annimmt, bzw. sehr stark ansteigt.
Zur Skizzierung des Funktionsgraphen wählen wir daher x-Werte zwischen -3 und +3 und setzen diese in die Originalfunktion f(x), sowie die ersten drei Ableitungen ein:
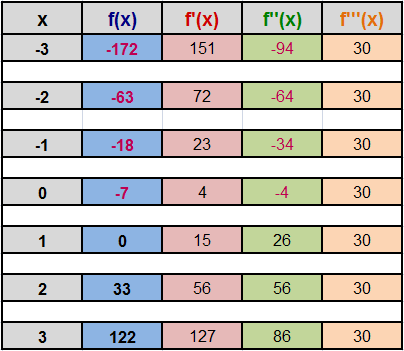
Um eine noch exaktere Zeichnung anzufertigen, kann man zusätzlich noch einige Zwischenwerte, z.B. im Intervall -2 > x > 2 ausrechnen.
11. Zeichnung des Funktionsgraphen
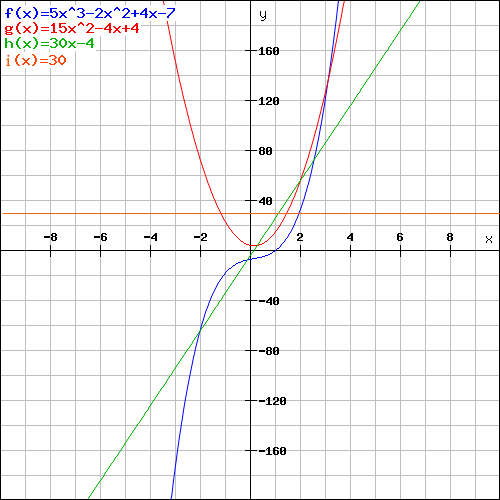
Eingezeichnet werden alle in den Schritten 1-10 ermittelten Punkte und Eigenschaften der Funktion sichtbar: Die Funktion verläuft zwischen von -∞ bis +∞ und hat bei x=1 eine Nullstelle.
Am Punkt W=(0,1333 | -6,4903) besitzt sie eine Wendestelle. An dem Punkt, wo die zweite Ableitung (grüne Gerade) ihre Nullstelle hat W=(0,1333 | -6,4903), befindet sich die Wendestelle der Funktion. An der Wendestelle wechseln nicht nur die Funktionswerte der zweiten Ableitung vom Negativen zum Positiven, sondern auch die Rechtskrümmung der Originalfunktion (blau) in eine Linkskrümmung.
Da f(x) an der Wendestelle keine Steigung hat, hat dort auch die erste Ableitungsfunktion einen Tiefpunkt, an den man eine waagerechte Tangente (= ohne Steigungswinkel) anlegen könnte.
Fazit
Mit der vollständigen Kurvendiskussion fand die Artikelreihe „Differentialrechnung in 5 Schritten“ ihren (vorläufigen) Abschluss. Vorläufig deshalb, weil es so viele verschiedene Aufgaben, Beispiele und Sonderfälle gibt, dass man sie alle gar nicht in eine Artikelreihe, geschweige denn einen Artikel packen kann.
Die Artikelreihe diente dem Zweck, eine Grundlegende Einführung ins Thema Differentialrechnung zu bieten und die wichtigsten Rechenschritte und Funktionsuntersuchungen anhand ausgewählter Beispiele zu veranschaulichen. Um im Thema jedoch noch sicher zu werden, hilft nur Übung – Und das am besten anhand möglichst verschiedener und auch schwieriger Beispiele. Um ein Gefühl zu den Zusammenhängen einer Funktion und ihren Ableitungen, sowie vom Aussehen der einzelnen Funktionen zu erhalten, empfiehlt es sich, beim Üben einen Funktionsplotter zu verwenden.
Zur Ergänzung dieser Artikelreihe werde ich in Zukunft sicherlich ab und zu noch weitere Artikel, in denen andere Ableitungsregeln, markante Punkte und Funktionseigenschaften zur Anwendung kommen, einstreuen ;).





Gute Arbeit, ich würde sagen Note 1
Hallo Lutz, vielen Dank ;)!
Hey Alicia,
ich habe gestern deinen Block gefunden und finde es suuuuper! Ich selbst habe mich eingeschrieben für wiwi vor einem Jahr, habe jedoch noch nicht angefangen da ich zu viel arbeite und reise. Jetzt habe ich mir aber fest vorgenommen es endlich zu Ende zu ziehen. Würde dich gern als eine erfahrene uni hagen – wiwi Studentin etwas fragen.
Ich habe vor 5 Jahren mein Abi gemacht mit der Spezialisierung in bwl im Ausland. Danach wollte ich weiter bwl an einer Uni machen, war jedoch für mich kaum möglich, da ich Sprachen lernen wollte und bin somit immer unterwegs durch die Welt gewesen. Jetzt wo ich unbedingt mein Bachelor und danach hoffentlich auch MBA machen möchte, fühle mich absolut Mathe unfähig. Habe mir sogar den Mathe Vorkurs bestellt und musste leider feststellen, dass ich nichtmal damit klar komme.
Jetzt nun endlich meine Frage, wie wahrscheinlich siehst du es, dass jemand wie ich, der Nachhilfe sogar für den Vorkurs braucht, kann dieses Studium zu Ende bringen? Ich meine das, was du oben so schon ausgerechnet hast ist für mich chinesisch! Kann man das Studium durchziehen mit einem eher im minus stehendem Wissen?
Ich habe aber Ökonomische Vorkenntnisse, arbeite als eine Führungskraft und spreche 5 Sprachen. Das einzige was mir fehlt, ist der Wirtschaftsstudium Titel, den ich für meine Kariere unbedingt brauche und persönlich auch haben möchte.
Vielen Dank
Deka
Hallo Deka,
vielen Dank für deinen Kommentar! Ich finde es super, dass du deine Karriere mit einem Wiwi-Studium voranbringen möchtest. Besonders wichtig und gut ist zunächst, dass du das Studium auch für dich persönlich machst, da das der Schlüssel ist, auch dauerhaft durchzuhalten.
Mathe ist bei Wiwi ein wichtiges Themenfeld, das sich praktisch durch alle Semester zieht und auf das du immer wieder stoßen wirst. Du solltest dich also darauf einstellen, dass Mathe ein stetiger Begleiter wird und dich dem Thema noch vor Bearbeitung der Studienunterlagen annehmen.
Es ist wichtig, von Anfang an gut mitzukommen, da die Studienhefte bereits bei den ersten Modulen grundlegende mathematische Kenntnisse voraussetzen. Damals, als ich angefangen habe, war ich Null vorbereitet und dachte, es würde schon alles in den Unterlagen erklärt werden. Dem war aber nicht so.
Ich glaube schon, dass du das Wiwi-Studium schaffen kannst, auch wenn du jetzt noch Probleme mit Mathe hast. Mach dich deswegen nicht verrückt und lass dich vor allem nicht runterziehen. So wie dir geht es vielen anderen Studenten auch.
Wichtig ist, dass du die mathematischen Grundlagen von Grund auf aufarbeitest, da der Vorkurs, den du besucht hast wahrscheinlich auch schon zu tief in die Materie gestartet ist. Ich habe Mathe damals mit Lecturio aufgefrischt und dort u.a. den Online-Kurs „Grundlagen Mathematik“ gemacht. Der fängt mit den grundlegenden Basic an, um Wirtschaftsmathe zu verstehen. Mir hat der Kurs sehr geholfen, da die Inhalte gut verständlich erklärt und anhand von zahlreichen Übungsaufgaben veranschaulicht werden.
Ich habe die Vorlesungen damals immer in Heften mitgeschrieben, sodass ich dort später immer etwas nachschlagen konnte. Später gibt es auch noch die aufbauenden Kurse „Analysis“ und „Algebra„.
An der Fernuni muss man in Bezug auf Mathe leider viel selbstständig erarbeiten. Wichtig ist, dass du eine Lernmethode findest, mit der du gut zurechtkommst und die Grundlagen nach und nach auffrischen kannst. Dann dürfte das Studium zu schaffen sein.
Falls dir das Konzept der Fernuni trotzdem nicht klarkommen solltest, wäre es eine Überlegung wert, an eine private Fernhochschule, wie die Euro-FH zu wechseln. Die Euro-FH hat sich auf BWL-Studiengänge spezialisiert und ist international ausgerichtet. Hier könnte der Studiengang Europäische Betriebswirtschaftslehre interessant für dich sein. Die Kosten sind zwar wesentlich höher, als an der Fernuni, dafür sind die Betreuungsleistungen umfangreicher.
Ich hoffe, dir etwas geholfen zu haben und wünsche dir viel Erfolg und vor allem Spaß bei deinem Studium!
Alles Liebe,
Alicia
Vielen Dank, Alicia!
Ich werde es erstmal versuchen und wenn ich sehe dass es nicht klappen sollte, werde versuchen direkt MBA an der Open University zu machen. Finde es aber komisch dass man in UK für MBA nur Mathe Basic braucht…
Liebe Grüße
Deka
Hallo Alica,
also jeder Blog der sich mit mathematischen Aufgaben beschäftigt bewegt sich auf didaktischem Spitzenniveau. Sehr sorgfälltig und verständlich formuliert. Und genau die richtigen Menge an Grafiken um das zu verdeutlichen was man eigentlich nur anhand von Bildern begreift.
Super :-]
Hey Stefan,
vielen herzlichen Dank für das Kompliment zum Artikel! Das „didaktische Spitzenniveau“, das du beschriebst, kenne ich nur allzu gut. In den Studienheften der Fernuni wimmelt es nur davon. Leider wird dabei das Fragezeichen über dem Kopf immer größer…
Daher freut es mich daher besonders, dass dir mein Artikel gut gefällt!
Viele Grüße,
Alicia
Hallo Alicia
Unter Punkt 6 wenn du die PQ Formel anwendest kommst du bei 7:5 auf 1,4 ,was ja richtig ist, gibst dann aber für q=1,5 an und rechnest damit weiter. Ich denke da hat sich ein kleiner Fehler eingeschlichen. Ansonsten sehr schön geschrieben, hat mir sehr geholfen.
Viele Grüße,
Andre
Hey Andre,
vielen Dank für den Hinweis! Hab mich wohl vertippt und fälschlicherweise mit 1,5 statt 1,4 weitergerechnet. Der Vertipper ist jetzt behoben.
Freut mich, dass dir der Artikel geholfen hat :)!
Viele Grüße,
Alicia
Vielen Dank für diese Erklärung! Ich gehe auf ein Gymnasium und seit einem Jahr habe ich Probleme in Mathe. Seitdem ich einen anderen Lehrer bekommen habe und es um Kurvendiskussionen geht. Ich habe nie den Zusammenhang zwischen allem verstanden! Dieser Eintrag ist jedoch so übersichtlich und einfach geschrieben, dass ich mir sehr schnell und ohne große Mühe alles erarbeiten konnte. Danke für diese Leistung ich hab durch das Lesen dieser Anleitung wirklich mehr gelernt als in 2 Jahren Schule in der Oberstufe auf einem Gymnasium. Herzlichen Dank und ein großes Lob!