Nachdem ich letztens so einen Klugscheißerartikel geschrieben habe und eigentlich dachte, die Kettenregel einigermaßen verstanden zu haben, hat mich seit gestern Nachmittag ein besonders schwerer Fall verfolgt.
Ich habe mir bei Lecturio einige Übungsaufgaben zu den Ableitungsregeln angeschaut und bin dann bei der vorletzten Aufgabe bis gerade eben hängen geblieben. Es ist wie so oft: Zuerst werden viele mehr oder weniger einfache Beispiele durchgerechnet, wenn es dann aber darauf ankommt, selbst Hand anzulegen und Aufgaben zur Kettenregel zu lösen, wird man schnell wieder auf den Boden der Tatsachen zurückgeholt.
Bei Lecturio sind die Aufgaben, die vorgerechnet werden alle ziemlich gut nachzuvollziehen, da man dort wirklich Schritt für Schritt vorgeht und den Lösungsweg gut versteht. So war es auch bei der vorletzten Aufgabe zur Kettenregel.
Diese lautete:
Leiten Sie folgende Funktion nach x ab:
Diese Funktion lässt sich sowohl mit der Quotientenregel, als auch mit der Kettenregel lösen. In der Online-Vorlesung wurde sie mit der Quotientenregel gelöst, nachdem das Ergebnis feststand wurde noch ergänzt, dass man hier auch die Kettenregel anwenden könne. Das könne man dann ja nochmal nachrechnen. Super.
Ich möchte in diesem Artikel beide Lösungswege einmal vorstellen, aber später vor allem noch mal auf das Problem mit der Kettenregel zurückkommen, da es in diesem Fall (jedenfalls für mich) besonders schwer und vor allem langwierig war, auf das richtige Ergebnis zu kommen.
Lösungsweg mit Quotientenregel:
Die Quotientenregel lautet in ihrer Urform:
(Zähler abgeleitet*Nenner – Nenner abgeleitet*Zähler / Nenner ins Quadrat). Wenn man sich das so ausgesprochen merkt, fällt es deutlich leichter, die Formel im Kopf zu behalten, als wenn man u´s und v´s einsetzt.
Setzt man für den Zähler und Nenner jetzt die Terme aus der Formel ein, sieht diese so aus:
Sieht zwar ein bisschen aggro aus, wir lösen den ganzen Kram jetzt aber nach und nach auf. Als erstes leiten wir die Zahl 2 ab, das ergibt Null. Gleichzeitig kann man anstelle der fünften Wurzel von x² auch x hoch 2/5 schreiben:
Da die Null mit dem Term des Nenners multipliziert wird, fällt dieser erste Ausdruck komplett weg. Übrig bleibt:
Jetzt gilt es, den oberen Term in der Klammer abzuleiten. Dafür multiplizieren wir die 3 vor dem x mit 2/5 und ziehen im Exponenten 1 ab (2/5 – 1):
Die (- 6/5) können wir gleich mit 2 multiplizieren und den Nenner ebenfalls so umformen, dass wir die Wurzel in einen Bruch umschreiben:
Denn Nenner können wir ebenfalls einfacher schreiben, indem wir die 3 quadrieren und den Exponenten von x (2/5) mit 2 multiplizieren, da gemäß Potentzgesetz:
Wir erhalten also:
Diesen gesamten Ausdruck können wir auch auf zwei Bruchstrichen schreiben. Wir machen einen Bruch für die Ausdrücke vor dem x und einen weiteren Bruch, auf dem wir lediglich den Faktor x mit Exponenten stehen haben:
Diese Schreibweise hätte jetzt nicht unbedingt sein müssen, erleichtert aber die Zusammenfassung dieser doch recht komplizierten Formel. Den ersten Bruch kann man jetzt ganz einfach ausrechnen und beim zweiten Bruch gleich ein weiteres Potenzgesetz anwenden, nämlich:
Wir erhalten dann:
Den erste Bruch können wir mit 3 kürzen und den Exponenten von x ausrechnen. Die Lösung lautet dann:
Äquivalent zu dieser Lösung kann man den zweiten Term auch noch in einem Bruch ausdrücken (siehe äquivalente Lösung 1) und zusätzlich auch noch den Exponenten im Nenner als Wurzel ausdrücken (siehe äquivalente Lösung 2):
Äquivalente Lösung 1:
Äquivalente Lösung 1:
So, endlich geschafft. Das wäre der Lösungsweg, wenn man die Quotientenregel anwendet. Jetzt kommen wir zum Lösungsweg mit der Kettenregel (der zum Glück nicht ganz so lang ist ;)):
Lösungsweg mit der Kettenregel:
Die Aufgabenstellung war: Leiten Sie diese Formel nach x ab.
Die Kettenregel wird bei verketteten oder verschachtelten Funktionen angewendet. Hierfür muss man erstmal erkennen, dass es sich überhaupt um eine verkettete Funktion handelt. Dies ist immer dann der Fall, wenn ein Term der Funktion „nicht nur“ x als Argument hat. Und das ist hier der Fall, denn das Argument der Wurzelfunktion ist nicht x, sondern x². Wir haben es hier also mit einer verketteten Funktion zu tun.
Die Ableitung einer verketteten Funktion wird anhand folgender Formel gebildet:
Um die äußere und die innere Ableitung zu erhalten, müssen zunächst der innere Term und der äußere Term der Funktion erkannt werden. Und das war nämlich bei mir ein echtes Problem, da wir es hier gleichzeitig mit einem Bruch und einer Wurzel zu tun haben. Der innere Term ist eigentlich immer der Term, der mit dem x am nächsten in Verbindung steht, hier also definitiv schon mal die „hoch 2“. Aber was ist mit der 5.Wurzel? Gehört die jetzt dazu oder nicht? Und wie leitet man einen Bruch ab? Fragen über Fragen, die jedoch nach vieler Hin- und Herrechnerei doch zum richtigen Ergebnis führten.
Zunächst einmal: Nein, die Wurzel gehört hier nicht zum inneren Term, sondern ist Bestandteil des äußeren Terms. Der innere Term ist also lediglich x², der Rest der äußere Term. Den inneren Term nennen wir einfacher halber mal u:
Die Ableitung einer verketteten Funktion erhält man durch die Ableitung des inneren Term multipliziert mit der Ableitung des äußeren Terms. Da der äußere Term jedoch noch etwas unappetitlich aussieht, formen wir diesen um, indem wir zunächst die Wurzel im Nenner auslösen und statt dessen einen Bruch schreiben:
So, jetzt ist schon mal die Wurzel weg, bleibt also noch der Bruch, der aber schon ganz anders aussieht, wenn man ihn vor das u mit dem Exponenten schreibt:
Wichtig dabei ist, dass vor dem Exponenten jetzt ein Minuszeichen steht, da er nicht mehr im Nenner steht.
Jetzt sieht der äußere Term schon etwas freundlicher aus und wir können die Ableitungen der beiden Terme bilden:
Zur gesamte Ableitung der verketteten Funktion müssen wir jetzt nur noch beide Ableitungen miteinander multiplizieren, wobei wir das u durch den ursprünglichen inneren Term, nämlich x² ersetzen:
Diesen Ausdruck können wir auch noch weiter vereinfachen, indem wir z.B. die Exponenten zusammenfassen:
Jetzt können wir die 2x mit dem erst Term multiplizieren und sehen dann gleich, dass die Lösung anhand der Kettenregel genau der Lösung mit der Quotientenregel entspricht (wäre sonst ja auch etwas schlecht ;)):
Auch hier kann den Exponenten wieder in Bruch und Wurzel ausdrücken (siehe Lösung Quotientenregel), aber ich gebe mich auch so zufrieden, hat schießlich lange genug gedauert ;).
Aber wie sagt man so schön: Ende gut, alles gut und nun geht´s weiter mit Lecturio…
Tipp:
Mehr Infos und Beispiele zum Thema Kettenregel gibt es in diesem Online-Tutorial von Lecturio.de: Die Kettenregel.
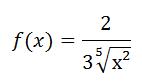
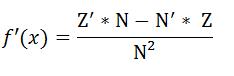
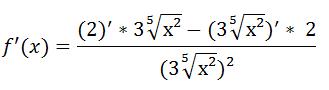
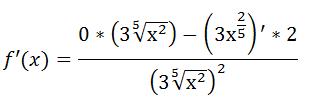
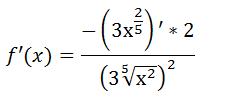
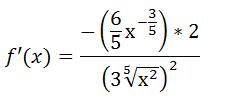
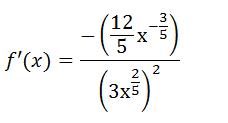
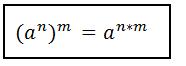
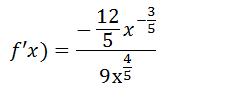
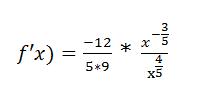
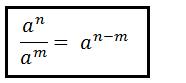
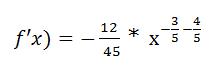
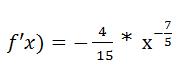
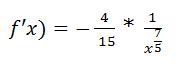
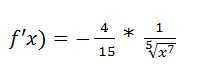
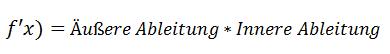
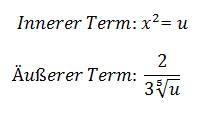
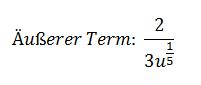


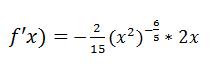
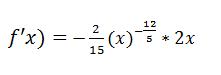
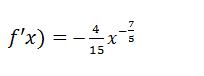



Irgendwie werden ein paar Klammern nicht richtig angezeigt…
Ich halte die Quotientenregel für eine Kanone, mit der auf Spatzen geschossen wird, wenn im Zähler nur eine Zahl und nichts mit x steht. Hier kann man nämlich die Potenzgesetze anwenden:
– die 5. Wurzel aus x^2 entspricht x^(2/5)
– da der Term im Nenner steht: 1/(x^2/5)) = x^(-2/5)
– mit dem Faktor 2/3 davor erhält man also f(x) = 2/3 * x^(-2/5)
Nun kann man die Regel für die Ableitung von Potenzfunktionen anwenden:
f'(x) = 2/3 * (-2/5) * x^(-2/5 – 1) = -4/15 * x^(-7/5)
Zum üben ist diese Aufgabe sicherlich sinnvoll, allerdings ist die Termumformung nach dem Ableiten komplizierter als vor dem Ableiten.
Hey,
hm, das Problem mit den Klammern konnte ich leider nicht erkennen^^…
Jedenfalls nicht im Chrome oder Firefox…
Mit der Quotientenregel hast du Recht, das Ding ist für dieses Beispiel im Prinzip wirklich etwas zu wuchtig, aber ich wollte es in erster Linie als Übung der QR und KR anführen.
Danke für deine kurze & knappe Lösung, an der man wieder sieht, dass viele Wege nach Rom führen… ;).
Viele Grüße,
Alicia
Ich habe mal ein paar Notizen an die Stellen gesetzt, an denen ich keine Klammer sehe (Firefox 4):
http://a.nnotate.com/docs/2011-05-22/579Tv1Pa/index.html
Vielleicht hilft dir das weiter.
Hey,
vielen Dank für den Screenshot und die Ergänzung der fehlenden Klammer vor beim „f(x)“. Hast Recht, da ist mir wohl irgendwo die eine Klammer vor dem x abhanden gekommen ;).
Ich bitte diese daher gedanklich zu ersetzen.
Vielen Dank für den Hinweis & Grüße,
Alicia