Nach den Grundlagen der Matrizenrechnung folgen nun einige grundlegende Aufgaben zu den verschiedenen Rechenregeln. Darunter sind Aufgaben zum Transponieren einer Matrix, Multiplikation mit einer reellen Zahl, einem Vektor oder einer anderen Matrix, sowie zu einigen grundlegenden Matrixpotenzen.
Aufgabe 1: Transponieren von Matrizen
Man transponiert eine Matrix Am,n, indem man ihre Zeilen- und Spaltenwerte vertauscht. Die transponierte Matrix drückt man mit einem hochgestellten T aus: ATm,n.
Beispiel 1:
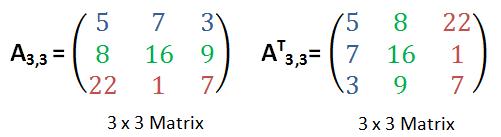
Transponiert man eine 3×3-Matrix, so ist auch die transponierte Matrix weiterhin eine 3×3-Matrix. Zeilen- und Spaltenzahl bleiben ja gleich.
Beispiel 2:
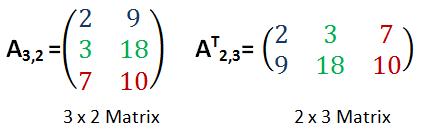
Anders sieht es bei einer 3×2-Matrix aus. Aus 3 Zeilen und 2 Spalten wird eine transponierte Matrix mit 3 Spalten und 2 Zeilen.
Beispiel 3:
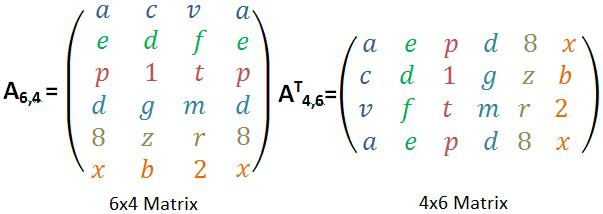
Natürlich kann man das Ganze auch mit größeren Matrizen machen, die entweder Zahlen oder Buchstaben enthalten. Der Prozess des Transponierens ist recht simpel, die meisten Fehler enstehen aus Unachtsamkeit oder Flüchtigkeit.
Beispiel 4:
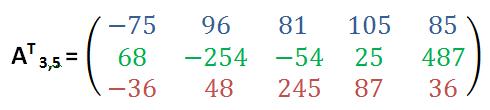
Das Transponieren kann auch anders herum angewendet werden, indem eine transformierte Matrix nochmals transponiert wird. Dadurch ergibt sich wieder die Ursprungsmatrix, denn (AT)T = A.

Beispiel 5:
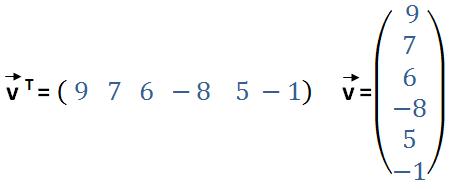
Auch eine Zeilen- oder Spaltenvektor, praktisch eine Matrix mit nur einer Zeile, bzw. Spalte, kann transponiert werden. In diesem Beispiel geht es wieder darum, einen bereits transponierten Vektor nochmals zu transponieren. Es ergibt sich wieder der ursprüngliche Spaltenvektor.
Aufgabe 2: Multiplikation von Matrizen mit einer reellen Zahl
Die Multiplikation eines Vektors mit einer reellen Zahl, einem sog. „Skalar“ gehört auch zu den einfach Rechenregeln. Dabei wird jeder Wert des Vektors mit dem jeweiligen Skalar multipliziert:
Beispiel 1:
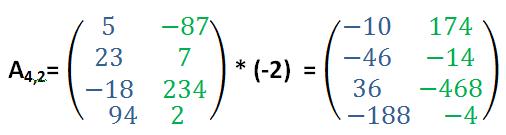
Die Aufgabenstellung könnte jedoch auch anders lauten, indem bei einer Matrix ein reeller Faktor ausgeklammert wird:
Beispiel 2:
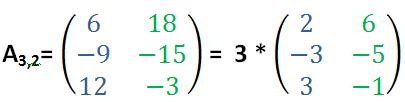
Oftmals wird das Ausklammern eines reellen Faktor verwendet, um kompliziertere Werte einfacher darzustellen, wie das folgende Beispiel zeigt:
Beispiel 3:
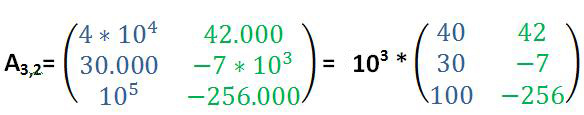
Multiplikation von Matrizen mit Vektoren
Um Matrizen mit einem Vektor (vergleichbar mit einer Matrix mit nur einer Zeile/Spalte) multiplizieren zu können, muss man die selbe Regel beachten, die auch bei der Matrizenmultiplikation gilt: Die Spaltenzahl der Matrix muss der Zeilenzahl des Vektors entsprechen.
Beispiel 1:
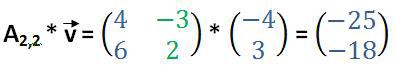
Eine 2×2-Matrix (=2 Spalten) kann mit diesem Spaltenvektor (= 2 Zeilen) multipliziert werden. Man geht bei der Vektormultiplikation nach dem Falkschen Schema vor. Die Rechenschritte lauten 4*(-4) + (-3)*(3) = -25 und 6*(-4) + 2*(3) = -18. Aus einer 2×2-Matrix wird durch Multiplikation mit einem Spaltenvektor (2×1-Matrix) ebenfalls ein Spaltenvektor (2x2-Matrix * 2x1-Matrix = 2×1-Matrix).
Beispiel 2:
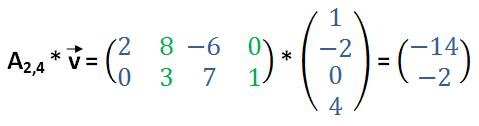
Genauso verhält es sich auch mit etwas größeren Matrizen. Hier haben wir eine 2×4-Matrix mit zwei Zeilen und vier Spalten. Um sie mit einem Vektor multiplizieren zu können, muss dieser vier Zeilen haben. Wir rechnen für die erste Zeile 2*1 + 8*(-2) + (-6)*0 + 0*4 = -14. Und für die zweiten Zeile des Ergebnisvektors: 0*1 + 3*(-2) + 7*0 + 1*4 = -2. Aus einer 2x4-Matrix multipliziert mit einem 4x1-Vektor entsteht ein 2×1-Vektor.
Beispiel 3:
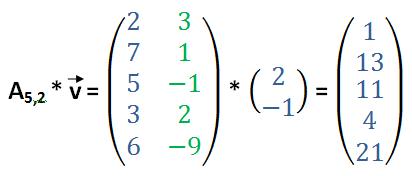
Eine 5×2-Matrix (2 Spalten) kann nur mit einem zweizeiligen Vektor multipliziert werden. Der Lösungsvektor ist demnach ein 5×1-Vektor. Die Werte für die erste Zeile ergeben sich aus den Rechenschritten 2*2 + 3* (-1) = 1, für die zweite Zeile aus 7*2 + 1*(-1) = 13, aus 5*2 + (-1)*(-1) = 11 für die dritte Zeile, für die vierte Zeile aus 3*2 + 2*(-1) = 4 und zu guter Letzt aus 6*2 + (-9)*(-1) = 21 für die fünfte Zeile.
Beispiel 4:
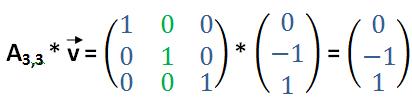
Eine 3×3-Matrix kann mit einem dreizeiligen Vektor multipliziert werden und ergibt (3x3 * 3*1) einen 3×1-Vektor. Wird eine sog. Einheitsmatrix mit einem Vektor multipliziert, ergibt sie immer den Vektor selbst. Die Rechenschritte sind: 1*0 + 0*(-1) + 0*1 = 0, 0*0 + 1*(-1) + 0*1 = -1 und 0*0 + 0*(-1) + 1*1 = 1.
Matrizenmultiplikation
Die Multiplikation von Matrizen miteinander, funktioniert genauso, wie die Multiplikation mit einem Vektor. Nur hat man hier nicht nur einen Spaltenwert, mit dem man multipliziert, sondern – je nach Größe der Matrix – mehrere Spalten, die die Sache manchmal etwas kompliziert aussehen lassen können.
Daher hilft es immer, eine Tabelle anzulegen und die einzelnen Ergebnisse dort zusammenzutragen. Hier einige Beispiele zur Matrizenmultiplikation:
Beispiel 1:
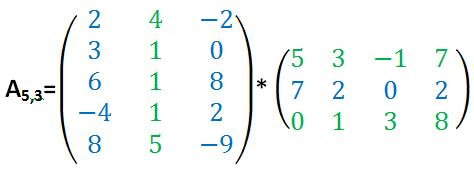
Diese beiden Matrizen können miteinander multipliziert werden, da die Spaltenanzahl der ersten Matrix (=3 Spalten) der Zeilenanzahl der zweiten Matrix (=3 Zeilen) entspricht. Die Matrizen werden multipliziert, indem man bei der ersten Zeile der ersten Matrix beginnt und jeden Wert mit den Werten der ersten Spalte der zweiten Matrix multipliziert. Anschließend wird daraus die Summe gebildet. Hört sich kompliziert an, ist es aber nicht.
Die folgende Tabelle soll den Rechenvorgang verdeutlichen:
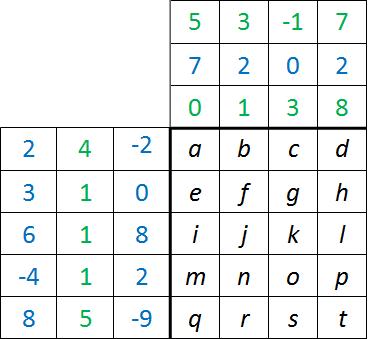
Aus einer 5x3-Matrix multipliziert mit einer 3x4-Matrix ergibt sich eine 5×4-Matrix. Damit kann man die Größe der Matrix bereits jetzt bestimmten. Da die ganze Rechnerei in der Tabelle etwas zu unübersichtlich wäre, führe ich die Rechenschritte für die Lösungswerte (Buchstaben) hier separat auf.
Für die erste Zeile der Lösungsmatrix:
- a = 2*5 + 4*7 + (-2)*0 = 10 + 28 + 0 = 38
- b =2*3 + 4*2 + (-2)*1 = 6 + 8 + (-2) = 12
- c =2*(-1) + 4*0 + (-2)*3 = (-2) + 0 + (-6) = -8
- d =2*7 + 4*2 + (-2)*8 = 14 + 8 + (-16) = 6
Für die Werte der zweiten Zeile der Lösungsmatrix:
- e = 3*5 + 1*7 + 0*0 = 15 + 7 + 0 = 22
- f =3*3 + 1*2 + 0*1 = 9+ 2 + 0 = 11
- g =3*(-1) + 1*0 + 0*3 = (-3) + 0 + 0 = -3
- h =3*7 + 1*2 + 0*8 = 21 + 2 + 0 = 23
Für die dritte Zeile der Lösungsmatrix:
- i = 6*5 + 1*7 + 8*0 = 30 + 7 + 0 = 37
- j =6*3 + 1*2 + 8*1 = 18 + 2 + 8 = 28
- k =6*(-1) + 1*0 + 8*3 = (-6) + 0 + 24 = 18
- l =6*7 + 1*2 + 8*8 = 42 + 2 + 64 = 108
In der vierten Zeile rechnen wir:
- m = (-4)*5 + 1*7 + 2*0 = (-20) + 7 + 0 = -13
- n =(-4)*3 + 1*2 + 2*1 = (-12) + 2 + 2 = -8
- o =(-4)*(-1) + 1*0 + 2*3 = 4 + 0 + 6 = 10
- p =(-4)*7 + 1*2 + 2*8 = (-28) + 2 + 16 = -10
Und in der fünften und letzten Zeile lauten die Rechenschritte:
- q = 8*5 + 5*7 + (-9)*0 = 40 + 35 + 0 = 75
- r =8*3 + 5*2 + (-9)*1 = 24 + 10 + (-9) = 25
- s =8*(-1) + 5*0 + (-9)*3 = (-8) + 0 + (-27) = -35
- t =8*7 + 5*2 + (-9)*8 = 56 + 10 + (-72) = -6
So, jetzt haben wir alle Werte der Lösungsmatrix ausgerechnet. Dieser sieht wie folgt aus:

Beispiel 2:
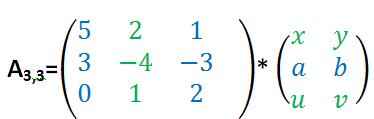
Beispiel 1 war bereits ein etwas ausführlicheres Beispiel, welches jedoch das Prinzip der Matrizenmultiplikation verdeutlichen sollte. Matrizen können auch miteinander multipliziert werden, wenn sie Zahlen und Buchstaben enthalten:
Auch hier kann man die einzelnen Rechenschritte in einer Tabelle festhalten:
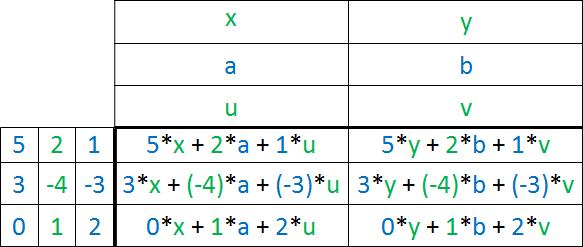
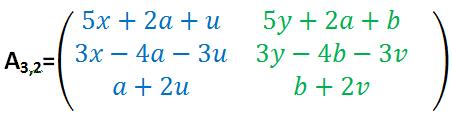
Aus der 3×3-Matrix mit Zahlen und der 3×2-Matrix aus Buchstaben ergibt sich eine 3*2- Lösungsmatrix aus Zahlen und Buchstaben:
Matrizenpotenzen
Als letztes Thema widmen wir uns dem Potenzieren von Matrizen. Doch auch das hört sich viel schlimmer an, als es letztendlich ist. Bei Matrizenpotenzen gilt die Formel:
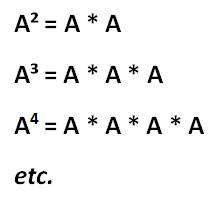
Beispiel 1:
Fangen wir mit dem quadrieren einer Matrix an. Dabei wird die Matrix einfach mit sich selbst Mal genommen.
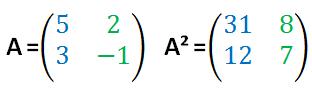
Der Rechenweg ergibt sich gemäß dem Falkschen Schema wie folgt:
Beispiel 2:
Will man eine Matrix hoch 3 nehmen, kann man ausgehend von der quadrierten Matrix A² diese wieder mit der Ursprungsmatrix A multiplizieren, denn A² * A = A³.
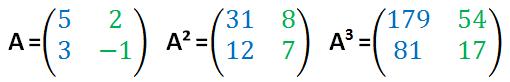
Der Rechenweg bei der Multiplikation von A² mit A sieht dann wie folgt aus:
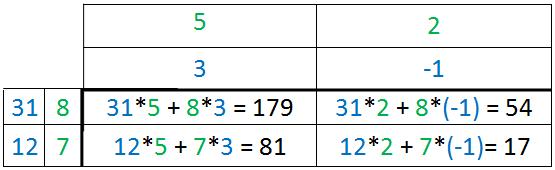
Beispiel 3:
Möchte man eine Matrix mit 4 potenzieren, so geht man mit denselben Schritten vor. Man sollte dabei immer das Potenzgesetz beachten:
Wenn man jetzt A4 ausrechnen möchte, kann man entweder A³*A rechnen oder aber auch A²*A². Das beide Rechenwege zum selben Ergebnis führen, zeigen die folgenden Tabellen:
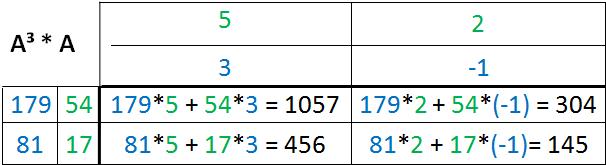
Dieselben Ergebnisse erhält man auch, wenn man A² mit A² multipliziert:
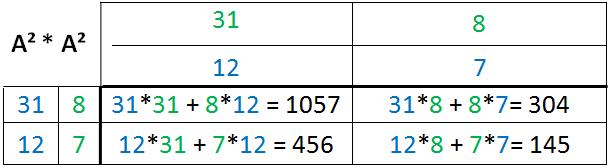
Als Lösung der einzelnen Potenzierungsstufen ergeben sich folgende Matrizen:
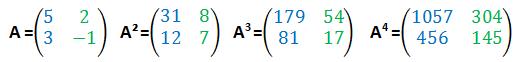
So kann man theoretisch auch mit höheren Potenzen vorgehen, wobei der Vorgang natürlich immer komplizierter wird. Aber Hauptsache, das Ergebnis stimmt ;).
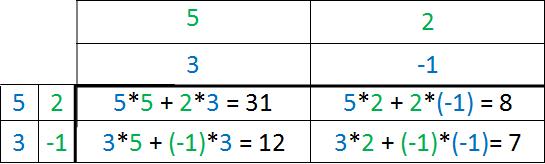
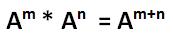


Wenn ich das im Studium hab, weiß ich wo ich nachschlagen muss 🙂
Hi Alicia,
vielen Dank für die kompakten Erklärungen bzw. generell für deinen Blog!
Ich habe nun mal angefangen für Mathe zu üben und dabei auch mit deinen Beispielen hier. Hat mir richtig geholfen, aber ich möchte kurz bemerken, dass sich im Beispiel 1 ein Fehler eingeschlichen hat. Ich komme als Ergebnis auf (-25, -18)T.
vg
Hey Basta,
vielen Dank für deinen Kommentar und den Hinweis zu dem Fehler. Welches Beispiel meinst du genau? Ich konnte den Fehler auf die Schnelle nicht finden.
Danke & Grüße,
Alicia
Hi,
bei Aufgabe 2 Beipiel 3 soll der Exponent doch bestimmt nicht negativ sein?
Wieder einmal Lob für dein Blog bin gerade mit dem Brückenkurs beschäftigt und das Kapitel über lineare Algebra am durcharbeiten daher kommt mir diese Seite mal wieder gerade recht.
Weiter so !
Gruss
Alex
Hey Alex!
Vielen Dank für deinen Kommentar, das positive Feedback und vor allem den Hinweis zu dem kleinen Fehler ;)! Habe ich soeben bereinigt.
Danke & Viele Grüße,
Alicia
Hi Alicia,
bedanke mich ebenfalls für den tollen Blog, der sehr aufwendig gestaltet ist und bestimmt viel Arbeit kostet.
Ich hoffe, Du kannst mein Selbstbewusstsein stärken:
Beim ersten Beispiel zur Matrizenmultiplikation sind Dir ein paar kleine Fehler unterlaufen, die man nur als Anfänger erkennt, wenn man die Aufgabe zur Übung von Anfang an genau nachrechnet….:
– Bei der Übertragung in das Falksche Schema wird aus der zweiten Spalte der Matrix (4 – 1 7 1 5) leider im Schema (4 1 1 1 5). Entsprechend verändern sich natürlich die Ergebnisse der zweiten und dritten Zeile der Ergebnismatrix zur Originalaufgabe.
– Weiterhin muss in Zeile 4 der Ergebnismatrix bei n =-8 und bei o = -10 herauskommen. Bei n liegt ein Rechenfehler vor, während Du bei o das Vorzeichen bei der -4 weglässt…
Hoffe, dass meine Anmerkungen korrekt sind, wollte keinesfalls „besserwissern“….Danke nochmals für die Mühen und beste Grüsse
Hey,
vielen Dank für den Hinweis, hast Recht, da haben sich bei der Übertragung ein paar kleine Fehler eingeschlichen. Ich habe die Ursprungsmatrix jetzt umgestellt und den Rechenweg, sowie die Lösungsmatrix entsprechend angepasst. Hoffe, jetzt passt alles ;)!
Danke & Viele Grüße,
Alicia
Prima, Danke!!! Fehlt nur noch Lösung n, da müsste es doch -8 heissen, oder? (-12)+2+2 = -8
Ich kann ja penetrant sein…besten Gruss
Was lange währt, wird endlich gut. So, jetzt aber ;)!
Danke nochmal & Grüße zurück!
Hey,
entweder hab ich ein Brett vorm Kopf, oder bei „Multiplikation von Matrizen mit Vektoren“, Beispiel 1 ist der Wurm drin 😀
Ich rechne da:
4x(-4) + (-3)x3 = -16-9 = -25
6x(-4) + 2×3 = -24+6 = -18
Der Ergebnisvektor ist bei mir also dann:
(-25)
(-18)
Ne Idee oder Einwände? ^^
Hey Danni,
du hast Recht, vielen Dank für den Hinweis! Ich habe die Matrix entsprechend korrigiert.
Liebe Grüße,
Alicia
Danke, Beispiel 1 war schön um noch mal die Matrixmultiplikation üben zu können.